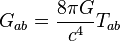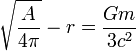algemene relativiteitstheorie
De algemene relativiteitstheorie is een meetkundige theorie van de zwaartekracht, die in 1916 door Albert Einstein werd gepubliceerd.[1][2] Het is de huidige beschrijving van de zwaartekracht in de moderne theoretische natuurkunde. De algemene relativiteitstheorie veralgemeent de speciale relativiteitstheorie en de gravitatiewet van Newton. Zij geeft een verenigde beschrijving van de zwaartekracht als een meetkundige eigenschap van ruimte en tijd (ook wel ruimtetijd). In het bijzonder houdt de kromming van de ruimtetijd direct verband met de vier-impuls (massa-energie en lineaire impuls) van de aanwezige materie en straling. De relatie wordt gespecificeerd door de Einstein-veldvergelijkingen, een systeem van partiële differentiaalvergelijkingen.
Veel voorspellingen van de algemene relativiteitstheorie verschillen aanzienlijk van die van de klassieke natuurkunde, met name die met betrekking tot de passage van tijd, de meetkunde van de ruimte, de beweging van lichamen in vrije val en de voortplanting van het licht. Voorbeelden van dergelijke verschillen zijn onder andere de gravitationele tijdsdilatatie, de gravitationele roodverschuiving van het licht en de gravitationele tijdsvertraging. De voorspellingen van de algemene relativiteitstheorie zijn tot op heden in alle waarnemingen en experimenten bevestigd. Hoewel de algemene relativiteitstheorie niet de enige relativistische theorie van de zwaartekracht is, is het de eenvoudigste theorie die consistent met de experimentele data is. Er blijven echter onbeantwoorde vragen, de meest fundamentele zijn hoe de algemene relativiteitstheorie kan worden verzoend met de wetten van de kwantummechanica om zo een volledige en zelfconsistente theorie van de kwantumzwaartekracht te produceren.
Einstein voorspelde correct dat licht van verre sterren dat langs de zon scheert in het zwaartekrachtsveld van de zon wordt afgebogen. Na de vele kwantitatieve experimentele bevestigingen van de theorie, werd de relativiteitstheorie beroemd als een elegante opvolger (verfijning) van de voorheen bekende zwaartekrachtstheorie van Newton.
Equivalentieprincipe
Uitgangspunt is het equivalentieprincipe. Waarnemers die uniform versneld worden zijn "equivalent" dus gelijkwaardig met andere waarnemers die stilstaan in een homogeen zwaartekrachtsveld. Dat wil zeggen dat de mechanica en andere natuurkundige wetten voor beide waarnemers dezelfde zijn. In de algemene relativiteitstheorie wordt de zwaartekracht niet als een kracht gezien die voldoet aan de Wetten van Newton, maar als een "schijnkracht" die het gevolg is van de kromming van de ruimte-tijd. Dit moet ook, want de wetten van Newton zouden een werking van de zwaartekracht toelaten sneller dan het licht, wat niet mogelijk is volgens de speciale relativiteitstheorie.
Ruimtekromming en zwaartekracht

De algemene relativiteitstheorie is een geometrische theorie, waarin wordt aangenomen dat zowel massa als energie de ruimtetijd doen krommen, en dat deze kromming de beweging van vrije deeltjes, waaronder ook het licht, beïnvloedt.
In zijn algemene relativiteitstheorie (1915) kwam Einstein met een nieuwe opvatting van de zwaartekracht. Hij stelde dat er geen verschil bestaat tussen een constante versnelling (trage massa) en een constante zwaartekracht (zware massa) (ga maar na: in een lift 9,8 m/s2 naar boven versnellen (ergens op een afgelegen plekje zonder zwaartekracht in de ruimte) geeft hetzelfde gevoel als op aarde te staan en met 9,8 N/kg (of ook m/s2) naar beneden te worden getrokken). Hij stelde ook dat materie (en elke andere vorm van energie) de ruimte vervormt. We vallen dus naar de aarde toe vanwege een kromming van de ruimte ten gevolge van de massa van de aarde. Dit is een grote wijziging ten opzichte van de ideeën van Newton. Deze theorie voorspelde afbuiging van sterrenlicht die tijdens een zonsverduistering in 1919 ook inderdaad waargenomen werden door Arthur Eddington. Ook biedt deze theorie een verklaring voor de precessie van de baan van Mercurius om de zon: dit is geen ellips zoals uit de Wetten van Kepler blijkt, maar wel een rozet.
Uitbreiding van de speciale relativiteitstheorie
De algemene relativiteitstheorie breidt de speciale relativiteitstheorie uit, door aan inertiaalstelsels een lokale betekenis te geven: een coördinatenstelsel geassocieerd met een waarnemer in vrije val. Een bijzonder geval hiervan is dat een algemene eenparige versnelling van massa's niet van een constant gravitatieveld onderscheiden kan worden. Meer algemeen kan gravitatie, als de versnelling van waarnemers in vrije val ten opzichte van elkaar, worden geïnterpreteerd als een gevolg van kromming van de ruimte.
Differentiaalmeetkunde
|
|
Wiskundig betekent het bestaan van lokale inertiaalstelsels dat de ruimtetijd een 4-dimensionale differentieerbare variëteit is, ongeveer zoals beschreven in de differentiaalmeetkunde van Bernhard Riemann. Bijgevolg maakt de algemene relativiteitstheorie gebruik van tensoren, omdat hiermee beweringen gedaan kunnen worden die onafhankelijk van coördinaten zijn. Eigenlijk zijn de gebruikte ruimten geen Riemann-variëteiten, maar Lorentz-variëteiten, omdat de metrische tensor niet positief definiet is, maar daarentegen signatuur 2 heeft (de enkelvoudige eigenwaarde in de tijd-richting is tegengesteld aan de drievoudige eigenwaarde in de ruimte-richtingen).
De theorie is gebaseerd op slechts een kleine groep formules en dit maakt de theorie erg elegant. Deze formules gebruiken echter ingewikkelde wiskundige concepten. Het belangrijkste resultaat van de algemene relativiteitstheorie vormt een stelsel partiële differentiaalvergelijkingen, de zogenaamde Einstein-vergelijkingen:
met:
- Gab is de Einstein-tensor
- Tab is de energie-momentum-tensor
Deze vergelijking stelt ruwweg dat de kromming van de ruimtetijd (het object links in bovenstaande vergelijking) gelijk is aan de energiedichtheid (het object rechts). Dat betekent dus dat massieve voorwerpen de ruimte krommen, en dat de banen van nabije voorwerpen afbuigen als gevolg van die kromming. Vaak wordt de vergelijking gemaakt met een trampoline. Stel je voor dat daarop een zwaar object ligt. Dat object vervormt het oppervlak van de trampoline. Als je dan een knikker over de trampoline laat rollen, wordt deze afgebogen (rolt niet meer rechtdoor) als gevolg van die kromming. Zwaartekracht werkt dus op precies dezelfde manier.
Het geometrische karakter van deze vergelijkingen, en de wiskundige eenvoud maakt van de relativiteitstheorie een uitzonderlijk elegante theorie .
Ruimtekromming
Meer eenvoudig gesteld is de kromming van de ruimte als volgt te vatten als uitbreiding van het bekende begrip kromming van een oppervlak. Stel we meten van een cirkel de omtrek en de doormeter (diameter) en we stellen vast dat hun verhouding niet pi is. Dan weten we, dat onze cirkel niet in een plat vlak ligt, maar bijvoorbeeld op een gekromd oppervlak zoals een bol en uit de afwijking kunnen we de kromtestraal van die bol bepalen. Stel we meten nu van een bol de oppervlakte A en de straal r. In een ruimte die geen massa bevat en dus niet gekromd is, geldt 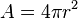 . Een ruimte die een massa m bevat is gekromd zodat
. Een ruimte die een massa m bevat is gekromd zodat
waarin G de gravitatieconstante en c de lichtsnelheid is. Die betrekking vervangt en verbetert de zwaartekrachtwet van Newton. Voor de aarde bedraagt het verschil 1,5 mm, voor de zon 500 m.
Tijddilatatie
Een gevolg van de algemene relativiteitstheorie is tijddilatatie, bijvoorbeeld dat een klok die h hoger staat in een zwaartekrachtveld met valversnelling g sneller loopt, namelijk met een factor:
Dit is aangetoond met behulp van een atoomklok. De algemene relativiteitstheorie geeft ook een elegant en juister alternatief voor de Wetten van Newton: als een voorwerp beweegt, dan zal de tijd ervoor trager lopen. Tijd en ruimte zijn dus complementair, hetgeen wil zeggen dat de som van de bewegingen van een voorwerp door tijd en ruimte altijd hetzelfde is en tevens gelijk aan de lichtsnelheid.[bron?] De weg die het voorwerp echt volgt is die weg die de tijd op de eigen klok zo groot mogelijk maakt. Aldus ontstaat een nieuwe dimensie, de ruimtetijd.
Experimentele toetsing
De volgende experimenten toonden direct of indirect de juistheid van relativiteitstheorie aan, in tegenstelling tot andere zwaartekrachtstheorieën zoals de voorheen gangbare Gravitatiewet van Newton:
- periheliumverschuiving van Mercurius
- Pound-Rebka-experiment (gravitationele roodverschuiving)
- tijdsverschil reizende en achterblijvende atoomklokken
- Radarreflectie aan planeten en ruimtesondes: tijdsdilatatie
- effect van Nordvedt
- pulsar in dubbelstersysteem (binary pulsar van Hulse en Taylor): zwaartekrachtsgolven
Ontwikkeling
Tot nog toe zijn alle experimenten in overeenstemming met de theorie, maar niet alle aspecten van de theorie zijn experimenteel getoetst. In het bijzonder wordt er wereldwijd met miniGrail gepoogd een zwaartekrachtsgolf waar te nemen, die als belangrijk dynamisch fenomeen door de theorie voorspeld wordt. Voorts is er een probleem met de kwantummechanica, daar er nog geen theorie is die gravitatie kwantumtheoretisch consistent beschrijft (zie Higgsboson en Graviton). In de meeste gevallen kunnen natuurkundigen met twee theorieën leven, de kwantummechanica op subatomaire schaal, de relativiteitstheorie op kosmische schaal, en 'simpele' Newtoniaanse mechanica op tussenliggende schalen, maar in enkele gevallen is de combinatie tussen sterke gravitatie en kleine schaal dusdanig dat beide theorieën invloed hebben, in het bijzonder bij zwarte gaten en in de eerste korte tijd na de oerknal.
Mogelijke oplossingen voor dit probleem zijn de Snaartheorie, de loop-kwantumzwaartekracht en als hypothese de allesomvattende theorie van alles.